2進数と基数変換の方法を解説
皆さんは「コンピュータは0と1で動いている。」という話を聞いた事があるでしょうか？
今現在、私達の暮らしにはコンピュータやネットワークが密接に関わっており、日常生活でのオンラインショッピングや調べ物、仕事での事務作業など、様々な事にコンピュータを使用しています。
このように様々な事が可能でとても便利な存在なので、コンピュータがどのような仕組みで動いているのかが気になる方も多いと思いますが、実際は0と1(電流が流れているか、流れていないか)の二種類しか使用していないのです。
(厳密に言えば電圧なども関係していますが…)
なので今回は、その基礎中の基礎である「2進数と基数変換」について解説したいと思います。
目次
2進数とは
そもそも2進数とは何かと疑問に思った方もいると思うので、簡単に2進数の説明をしていこうと思います。
私達の普段の生活で使用されている数字は「0～9」までの数字で構成されており、「9」から1つ増えると「10」となり、桁が一つ繰り上がります。
この、「何個目の数字になったら繰り上がるのか」というのを表した物が～進数という物で、私達の生活になじみ深い「10」になったら繰り上がる物を10進数と言い、コンピュータ内で使用されているのは「2」になったら繰り上がる2進数です。
2進数の数え方
2進数は0と1のみ構成されているので、2進数の仕組みを知らない人が見ると戸惑うかもしれませんが、その2進数の仕組みさえ分かってしまえば簡単です。
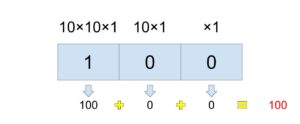
例えば、10進数で3の位に1という正数が入っているとしたら、「10×10×1が1個存在している」という事になるので、答えが100になるのが分かると思います。
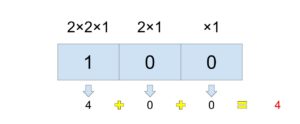
2進数の場合でもそれは同じで、例えば3の位に1が入っているとしたら、「2×2×1が1つ存在している」という事になるので答えは4になります。
なので、2進数の数字を10進数で数える場合は、「2^(桁数-1)×桁内の整数」で各桁の数値を出し、それらの答えを合計する事で求める事が出来ます。
2進数の小数点以下の場合
2進数で整数の場合は「2^(桁数-1)×桁内の整数」で求める事が出来るのですが、小数点の場合も同じ方法で求める事が可能です。
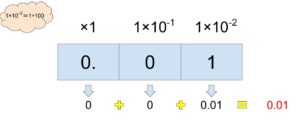
例えば10進数で0.01という数の場合は、「1÷10÷10×1」という式に置き換える事が出来ると思います。
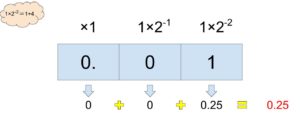
2進数の場合も同じで、0.01という2進数の数を求める場合は「1÷2÷2×1」なので、0.25になります。
整数の場合はその桁の数-1の分だけ掛けていましたが、小数の場合は逆に割って求める事になるので注意して下さい。
2進数以外の基数
～進数というのは「何個目の数字になったら繰り上がるのか」を表しているので、やろうと思えば3進数や21進数など、様々な進数で数を表す事が可能です。
ですが、その中でも特に使用されているのが、2進数と互換性を持つ「8進数」と「16進数」で、それぞれ2進数の状態から簡単に変換する事が出来ます。
ちなみに、16進数は16になったら桁が繰り上がるのですが、一桁目で「10」や「11」などの数字を使う訳にもいかないので、「A(10)」「B(11)」「C(12)」という風にして数字を表していきます。なので、10進数の27という数字を表す場合は「1B」という書き方です。
それぞれの進数と10進数の対応
イメージしやすい様に、それぞれの進数の値と10進数の値を対応させてみようと思います。
【2進数】
| 10進数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 2進数 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | … |
【8進数】
| 10進数 | 0 | 1 | ～ | 6 | 7 | 8 | 9 | 10 | … |
| 8進数 | 0 | 1 | ～ | 6 | 7 | 10 | 11 | 12 | … |
【16進数】
| 10進数 | 0 | 1 | ～ | 8 | 9 | 10 | 11 | 12 | ⇒ |
| 16進数 | 0 | 1 | ～ | 8 | 9 | A | B | C | ⇒ |
| ⇒ | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | … |
| ⇒ | D | E | F | 10 | 11 | 12 | 13 | 14 | … |
コンピュータの中では2進数が使用されているのですが、それではすぐに桁数が多くなってしまい分かりにくくなってしまう為、人間が理解しやすい表現として2進数と互換性のある8進数や16進数が使用される事があります。
基数変換とは
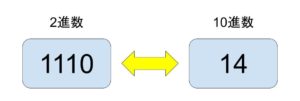
基数変換とは、2進数の数値を8進数に変えたり、16進数の数値を10進数に変えたりして、文字通り基数を違う物に変換する事を言います。
通常基数変換をする場合、その数に掛けたり割ったりして求めていくのですが、2進数と8進数や2進数と16進数の様に、元々の基数(2)とべき乗の関係(‘2’^3=’8’)(‘2’^4=’16’)にあたる基数に変換する際には簡単に求める事が可能です。
基数変換の具体的な方法
一般的な基数変換の方法は、整数と小数点以下の場合で求め方が異なります。
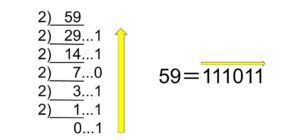
まず整数の場合は、元の値から基数で割って余りを出していき、答えが0になったら余りの数値を下から準に書く事で求められます。
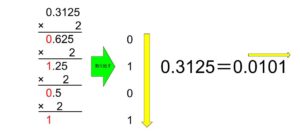
次に小数の場合ですが、整数の時とは逆に、元の小数の値から基数を掛けて整数を抜き出していき、答えが全て整数になったら抜き出した整数の値を上から準に書いていく事で求める事が可能です。
この時、整数の場合は出てきた余りを上から書いていきましたが、小数の場合は上から準に書いていくので間違わない様に注意して下さい。
べき乗の関係にある進数の基数変換
通常の場合とは異なり、べき乗の関係にある数同士の基数変換ならば基数変換を簡単に行う事が出来ます。
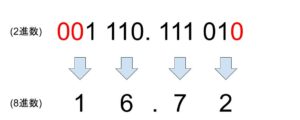
例えば、2進数と8進数の場合だと、8は2の3乗なので2進数の値から3個ずつに分けていき、それぞれの数を求める事で8進数にする事が可能です。
ちなみにこの逆の方法も可能で、8進数から2進数への変換の場合は、それぞれの桁の数を3桁の2進数にする事で求められます。
とりあえず数をこなして慣れよう
2進数の基数変換などは頻繁に使用する事になると思うので、早い段階から問題数をこなして慣れる様にしておきましよう。
慣れない内は間違いが多くなると思いますが、決して難易度の高い事をしている訳ではないので、早い段階から慣れる様にしておくと、これから情報系の分野を学ぶ人にとっては大きなアドバンテージになると思います。
インターネット上には様々な基数変換の問題が転がっていますし、書店で基本情報技術者関連の本もあると思うので、気になった方は見てみて下さい。
最後に
今回は2進数と基数変換について書いてみました。
参考になれば幸いです。
